[Series] Arithmetic Series of Higher Order
By: Tao Steven Zheng (鄭濤)
【Problem】
Chinese mathematicians of the Song-Yuan period (960 - 1368 AD) investigated finite sums related to the diagonals of Jia Xian's triangle (arithmetic triangle). The following list given names of several finite sums found in Zhu Shijie’s "Suanxue Qimeng" (1299) and "SiYuan Yujian" (1303).
"Suanxue Qimeng" 算學(xué)啟蒙 (Introduction to Mathematics)
"SiYuan Yujian" 四元玉監(jiān) (Jade Mirror of the Four Unknowns)
茭草垛
落一形垛
撒星形垛
撒星更落一形垛
These finite sums are called arithmetic series of higher order, which follow the general pattern
Alternatively this can be expressed as
Prove this identity.
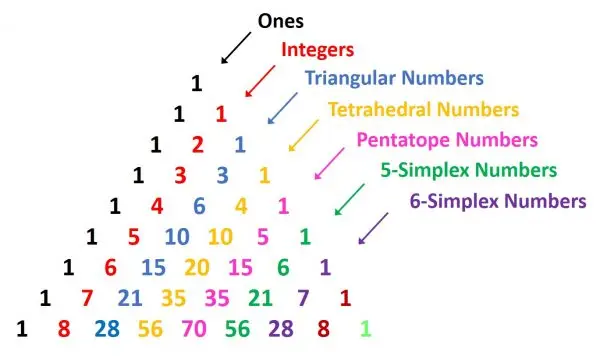

【Solution】
Observe that , hence,
By the binomial identity , we get
Following this step-pattern
until we reach the final term
Therefore,
標(biāo)簽:

